21. Multiple Integrals in Curvilinear Coordinates
c. Integrating in Spherical Coordinates
4. Converting & Mixing, Rectangular & Spherical Coordinates
Sometimes it is useful to use spherical coordinates instead of rectangular coordinates when computing an integral. Other times it is best to use rectangular coordinates for one part of an integral and spherical coordinates for another part.
Converting Rectangular to Spherical Coordinates
Sometimes by converting to spherical coordinates, we can simplify the integral greatly.
Use spherical coordinates to find the mass of the ice cream cone between the cone \(z=\sqrt{x^2+y^2}\) and the hemisphere \(z=\sqrt{50-x^2-y^2}\) if the mass density is \(\delta=z(x^2+y^2)\).
This problem was done in cylindrical coordinates in an exercise on a previous page. Notice how much easier the spherical computation is.
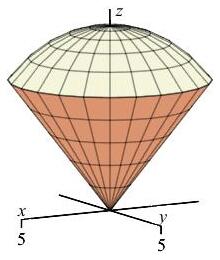
The mass of a region is the integral of the density function over the region: \[ M=\iiint \delta\,dV=\iiint z(x^2+y^2)\,dV \] The density and volume element in spherical coordinates are: \[\begin{aligned} \delta&=z(x^2+y^2)=(\rho\cos\phi)(\rho^2\sin^2\phi)=\rho^3\cos\phi\sin^2\phi \\ dV&=\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \end{aligned}\] The cone is: \[ z=\sqrt{x^2+y^2} \quad \Rightarrow \quad \rho\cos\phi=\rho\sin\phi \quad \Rightarrow \quad \tan\phi=1 \quad \Rightarrow \quad \phi=\dfrac{\pi}{4} \] The hemisphere is \[ z=\sqrt{50-x^2-y^2} \quad \Rightarrow \quad x^2+y^2+z^2=50 \quad \Rightarrow \quad \rho=\sqrt{50} \] So the mass is: \[\begin{aligned} M&=\int_0^{2\pi}\int_0^{\pi/4}\int_0^{\sqrt{50}} (\rho^3\cos\phi\sin^2\phi)\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=\int_0^{2\pi}\int_0^{\pi/4}\int_0^{\sqrt{50}} \rho^5\cos\phi\sin^3\phi\,d\rho\,d\phi\,d\theta \\ &=2\pi \left[\dfrac{\sin^4\phi}{4}\right]_0^{\pi/4} \left[\dfrac{\rho^6}{6}\right]_0^{\sqrt{50}} =2\pi\dfrac{1}{4}\left(\dfrac{1}{\sqrt{2}}\right)^4\dfrac{\sqrt{50}^{\,6}}{6}\\ &=2\pi\dfrac{1}{4}\dfrac{1}{4}\dfrac{50^3}{6} =\dfrac{5^6}{6}\pi \end{aligned}\]
Find the volume of the ice cream cone in the previous problem.
\(V=2\pi\left(1-\dfrac{1}{\sqrt{2}}\right)\dfrac{\sqrt{50}^3}{3}\)
This is the same computation, just leaving out the density: \[\begin{aligned} V&=\iiint\limits_R 1\,dV =\int_0^{2\pi}\int_0^{\pi/4}\int_0^{\sqrt{50}} \rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=2\pi\left[-\cos\phi\dfrac{}{}\right]_0^{\pi/4} \left[\dfrac{\rho^3}{3}\right]_0^{\sqrt{50}} =2\pi\left(1-\dfrac{1}{\sqrt{2}}\right)\dfrac{\sqrt{50}^3}{3} \end{aligned}\]
Mixing Rectangular, Cylindrical and Spherical Coordinates
Sometimes one integral should be done in rectangular coordinates and another should be done in spherical coordinates, such as in the example below.
Consider the hemisphere \(0 \le z \le \sqrt{64-x^2-y^2}\) that has a rectangular box cut out of it with dimensions of \(-3 \le x \le 3\) and \(-3 \le y \le 3\) and \(0 \le z \le 3\). Find the average value of the density of the region between the rectangular box and the sphere if the density is given by \(\delta=z\).
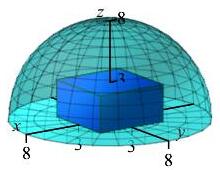
We divide the solution into several steps:
- Find the volume and mass of the hemisphere (with no box cut out).
- Find the volume and mass of the box that is cut out.
- Subtract the volume of the box from the volume of the hemisphere to find the volume of the 3D region between them.
- Subtract the mass of the box from the mass of the hemisphere to find the mass of the 3D region between them.
- Divide the mass of the region by the volume of the region to get the average density.
First, we use geometry to find the volume of the sphere and use spherical coordinates to find the mass of the sphere. \[ V_\text{hemisphere} =\dfrac{1}{2}\left(\dfrac{4}{3}\pi r^3\right) =\dfrac{2}{3}\pi(8)^3 =\dfrac{1024}{3}\pi \] The density is \(\delta=z=\rho\cos\phi\). So the mass of the sphere is: \[\begin{aligned} M_\text{hemisphere} &=\iiint \delta\,dV =\int_0^{2\pi}\int_0^{\pi/2}\int_0^8 (\rho\cos\phi)\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=2\pi\int_0^{\pi/2} \sin\phi\cos\phi\,d\phi\int_0^8\rho^3\,d\rho \\ &=2\pi\left[\dfrac{\sin^2\phi}{2}\right]_0^{\pi/2} \left[\dfrac{\rho^4}{4}\right]_0^8 =2\pi\left(\dfrac{1}{2}\right)\dfrac{8^4}{4} =1024\pi \end{aligned}\]
Using rectangular coordinates, we can easily find the volume of the box: \[ V_\text{box}=6\cdot6\cdot3=108 \] And the mass of the box is \[\begin{aligned} M_\text{box} &=\iiint \delta\,dV=\int_{-3}^3\int_{-3}^3\int_0^3 z\,dz\,dy\,dx \\ &=36\left[\dfrac{z^2}{2}\right]_0^3 =162 \end{aligned}\]
Next we subtract the volume of the box from the volume of the sphere: \[ V_\text{region}=V_\text{hemisphere}-V_\text{box} =\dfrac{1024}{3}\pi-108\approx964.3 \]
Next we subtract the mass of the box from the mass of the hemisphere: \[ M_\text{region}=M_\text{hemisphere}-M_\text{box} =1024\pi-162\approx3055.0 \]
Finally, we divide the total mass of the region by the total volume of the region: \[ \delta_\text{ave}=\dfrac{M_\text{region}}{V_\text{region}} =\dfrac{1024\pi-162}{\dfrac{1024}{3}\pi-108}\approx3.168 \]
The density \(\delta=z\) ranges from \(0\) to \(8\). So \(\delta_\text{ave}\approx3.168\) is within this range.
A hole of radius \(2\) is drilled through a sphere of radius \(4\) as shown in the plot. Find the volume of the remaining solid.
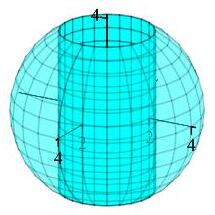
You know the volume of a sphere. You need to compute the volume of the hole drilled out. Careful, it is not just a cylinder!
\(V = 32\pi\sqrt{3} \approx 174.12\)
Let \(V_\text{sphere}\) and \(V_\text{hole}\) represent the volumes of the sphere and the hole drilled out of it, respectively. Then \[ V = V_\text{sphere} - V_\text{hole} \] We can easily compute that a sphere of radius \(4\) has volume: \[ V_\text{sphere} = \dfrac{4}{3}\pi(4)^3 = \dfrac{256}{3}\pi \] To find \(V_\text{hole}\), we will integrate using cylindrical coordinates. The volume of a 3D region in cylindrical coordinates is given by the formula \[\begin{aligned} V_\text{hole} = \iiint r \,dz\,dr\,d\theta \end{aligned}\]
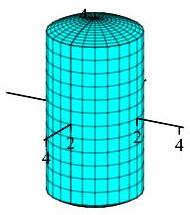
The sphere can be paramaterized as \(z^2 + r^2 = 16\), so our bounds are \(-\sqrt{16-r^2} \le z \le \sqrt{16-r^2} \) along with \(0 \le r \le 2\) and \(0 \le \theta \le 2\pi\). Thus \[\begin{aligned} V_\text{hole} &= \int_0^{2\pi} \int_0^2 \int_{-\sqrt{16-r^2}}^{\sqrt{16-r^2}} r \,dz\,dr\,d\theta \\ &= \int_0^{2\pi} d\theta \int_0^2 \left[\rule{0pt}{10pt}rz\right]_{z=-\sqrt{16-r^2}}^{z=\sqrt{16-r^2}}\,dr \\ &= 4\pi \int_0^2 r\sqrt{16-r^2}\,dr \end{aligned}\] We use the substitution \(u=16-r^2\). Then \(du = -2r\,dr\), so \[\begin{aligned} V_\text{hole} &= 4\pi \int_0^2 r\sqrt{16-r^2}\,dr = -2 \pi \int_{16}^{12} \sqrt{u}\,du = 2 \pi \int_{12}^{16} \sqrt{u}\,du \\ &= 2\pi \left[\dfrac{2}{3}u^{3/2} \right]_{12}^{16} = \dfrac{4}{3}\pi(64-24\sqrt{3}) = \dfrac{256}{3}\pi - 32\pi\sqrt{3} \end{aligned}\] Finally, we can calculate \[ V = V_\text{sphere} - V_\text{hole} = \dfrac{256}{3}\pi - (\dfrac{256}{3}\pi - 32\pi\sqrt{3}) = 32\pi\sqrt{3} \approx 174.12 \]
mj
Rather than compute the volume of the sphere and subtract the volume of the hole, we can directly compute the volume of the remaining piece directly in cylindrical coordinates: \[\begin{aligned} V &= \int_0^{2\pi} \int_2^4 \int_{-\sqrt{16-r^2}}^{\sqrt{16-r^2}} r \,dz\,dr\,d\theta = \int_0^{2\pi} d\theta \int_2^4 \left[\rule{0pt}{10pt}rz\right]_{z=-\sqrt{16-r^2}}^{z=\sqrt{16-r^2}}\,dr \\ &= 4\pi \int_2^4 r\sqrt{16-r^2}\,dr = -2 \pi \int_{12}^0 \sqrt{u}\,du \\ &= 2 \pi \int_0^{12} \sqrt{u}\,du = 2\pi \left[\dfrac{2}{3}u^{3/2} \right]_0^{12} \\ &= \dfrac{4}{3}\pi(24\sqrt{3}) =32\pi\sqrt{3} \end{aligned}\] This was in fact easier!
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum